Oletame, et oleme leidnud endale investeerimisobjekti ning mõtleme, et pargime oma raha sellesse järgnevad 5 aastat või kauemgi. Investeerimine võib olla keerukas ning isegi tulusad objektid võivad tuua meile rohkem kahju kui kasu. Vaadates varasid nagu näiteks NVIDIA või Microsoft, võib meil tekkida tunne, et need on justkui head valikud pikaajaliseks investeerimiseks – ostad igal kuul mõned osakud juurde, pärast pensionieas hea maha müüa.
Mõte on tore, kuid arvestades hinna kõikumist ja turu muutuseid, ei pruugi me saada oma investeeringust lõpuks seda tootlust, mida oleme lootnud. Teisisõnu see, et S&P 500 on tõusnud viimase 5 aasta jooksul umbes 90%, ei tähenda, et meie portfell tõuseb samas tempos (isegi kui me ostaksime ajamasina, läheksime tagasi 5 aastat ning pargiksime 100€ iga kuu S&P 500 indeksisse, ei ole meie tootlus sama, mis indeksil) – indeksi tootlus on alati suurem, kui meie tegelik tootlus.
Seda ei muuda me ka siis, kui arvutame oma hinnangulise tootluse läbi liitintressi valemi. Liitintressi valem saab arvesse võtta ainult fikseeritud suurusega intressimäära (võime selle asendada tootluse %-ga). Erinevatel hinnatasanditel indeksisse positsioonide soetamisel muutub meie tootluse % vastavalt hindadele – kõikuva tootluse %-ga pole liitintressi adekvaatselt võimalik arvutada.
Selleks, et teemat paremini mõista, vaatame korraks raha ajalise väärtuse põhimõtet. Raha ajaline väärtus (time value of money) – raha täna on vähem väärt kui homme. Seda tõlgendatakse tihtipeale arvamusega, et inflatsioon sööb meie rahalise väärtuse ära, mistõttu on raha homme vähem väärt. See pole aga kõige korrektsem termin, sest inflatsioon võib töötada kahes suunas – inflatsioon ehk hindu tõstev mehhanism ja deflatsioon ehk hindu alandav mehhanism. Seega kui hinnad langevad, saame me oma eurode eest rohkem osta.
Raha väärtus ajas otseselt ei lange – kasutusel olev FIAT valuuta omab täpselt samasuurt nimiväärtust homme, nagu talle on antud täna ehk 1 euro = 1 euro ka aasta või kahe pärast. Raha ajalise väärtuse kontseptsioon viitab sisult eelkõige sellele, et tänane investeering on homme kallim, sest investeeringu väärtus kasvab – täna võime me investeerida 1000 eurot 10% tootlusega ning olla aasta pärast 100 euro võrra rikkamad, kuid investeerides järgmisel aastal sellesse instrumenti peame me arvestama juba 1100-eurose hinnaga, mis minevikku tõlgendades tähendab, et me kaotasime 100 eurot, sest me ei investeerinud raha kohe.
Sama põhimõtet võime me näha kaupade soetamisel, kuid siin töötab asi vastupidi. See tähendab, et tänane kaup on homme vähem väärt. Selle põhjuseks ei ole aga raha väärtuse langemine, vaid selle põhjustab uute kaupade turule tulemine – need pakuvad eelmisest versioonist suuremat kasulikkust tarbijale. Hüpoteetiliselt: kui tootearendust ei toimuks, ei kaotaks vanad tooted oma väärtust nii kiiresti (arvestama peab endiselt sellega, et vana ja uue vahel on erinevused ning kasutatud asjad pole nii ihaldusväärsed kui uued).
Raha ajalise väärtuse põhimõte on laialdaselt seotud intressiarvestusega, mitte otseselt inflatsiooniga ning selle tõestab ära neto nüüdisväärtuse valem ehk NPV. Neto nüüdisväärtus uurib suhet asjade tänase väärtuse ja intressimäärade vahel. See on võimekas tööriist, millega hinnata erinevate tehingute tänast väärtust, tingimusel, et nendest saadav tulu laekub tulevikus. Ehk kui me investeerime kuhugi ning tahame teada, kas see on tulevikus tulu toov või mitte.

Kuidas seda mõista?
Eeldame, et soovime täna osta iPhone’i, mis maksab 1 000€ ning me tahame teada, kui palju see sama mudel on väärt tulevikus (uuena ostes võrreldes uute tulevaste mudelitega).
Sellisel juhul võime me panna selle valemisse ja saada vastuse. LHV panga kalkulaatori järgi oleks intressimäär tänasele laenule 10,9%, taandame selle 11% juurde lihtsalt arvutamise mugandamiseks.
Pannes selle valemisse koos 1 000 euroga (iPhone’i hind) saame me järgneva tulemuse:
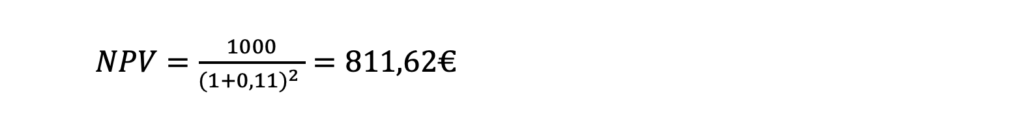
See näitab tänase iPhone’i mudeli väärtust 2 aasta pärast.
Vaadates iPhone’i turgu tänasel päeval ja jättes arvestamata allahindlused (need ei näita toote õiglast turuhinda, vaid on turundusmeetmed), on näha, et täishinnaga iPhone 15 maksab täna 989€ ja iPhone 13 maksab 769€, mis mahub ideaalselt meie algsesse võrdlusesse, milleks oli 1 000€ ja 811,62€.
Oleks me kasutanud poes märgitud turuhinda, oleks meie kalkulatsioon andnud natukene täpsema vastuse, kuigi NPV pole kunagi 100% täpne. Funktsioon pole täiuslik, kuid me ei ootagi sellest ideaalset ennustust, vaid suunaviita tuleviku väärtuse hindamisel, milleks on see funktsioon enamgi kui võimeline.
NPV arvutuse kaudu on näha selget korrelatsiooni raha ajalise väärtuse ja intressimäärade vahel. Me võime kasutada siin inflatsioonimäära, kuid sellisel juhul ei suudaks me adekvaatselt hinnata erinevate varaklasside mõju meie ostujõule, sest inflatsioon koondab endasse kõikide turuosaliste hinnamuutused. Samas intressimäär on palju universaalsem. Viimase aja võlakirjade intress on 11% ringis, sama on järelmaksude oma.
Olles raha ajalise väärtuse kontseptsiooni avanud, vaatame, kuidas võiks seda kasutada, et hinnata investeeringu tulevikuväärtust.
Mida see üldse tähendab? Investeerides, tahame me teada, kas investeering tasub ennast ära või kaotame me sellega raha. Selle hindamiseks võimegi rakendada NPV valemit ning otsustada tulemuse järgi, kas tegemist on tulusa investeeringuga või mitte.
Kui tavaliselt otsitakse NPV-d, üritatakse see panna võrduma nulliga. Näiteks IRR kontrollimisel vähendatakse tuleviku rahavoogusid sisemise intressimäära jagu ning kui oleme sisemise intressimäära arvestanud õigesti, on meie tulemuseks 0, sest investeeringu alguses ei tohiks meil olla rohkem ega vähem raha meie algkapitalist.
Seega võime eeldada, et kui me rakendame NPV arvestust investeeringu hindamisele, tahame me näha tulemust, mis on suurem kui 0, sest me ootame, et meie raha oleks tulevikuga võrreldes rohkem väärt, kui on selle „turuväärtus“ samal ajahetkel.
Kõlab keeruliselt? Ütleme sedasi: investeerides tahame saavutada olukorra, kus meil on võimalik osta rohkem kui inimestel, kes ei investeeri.
Kuidas seda rakendada? NPV-d rakendatakse erinevalt ning leidub neid, kes ei pea seda kõige paremaks indikaatoriks, sest NPV sellisel viisil ei näita meile meie investeeringu tegelikku väärtust, tihtipeale annab vastuseks tulemuse kümnendmurrus (0,1 või 1,02 või -0,8 jne). See tähendab, et me ei näe oma investeeringu koguväärtust, vaid hindame, kas see on suurem või väiksem algväärtusest.
Suurem kui algväärtus tähendab, et investeering on tulus ning me võime seda kaaluda ning vastupidine tähendab, et me peaksime sellest hoiduma. Ehk see on pelgalt tööriist, mille abil otsustada.
Tasub muidugi meeles pidada, et tegemist on kõigest kalkulatsiooniga ning ükski kalkulatsioon, olenemata oma täpsusest, pole piisav, et näha ette iga võimalikku tulemit. See tähendab, et isegi antud kalkulatsiooni tulemust tuleks käsitleda ainult ühe näitajana ning enne tegeliku otsuse langetamist kaaluma ka teisi lahendeid.
Selleks, et oma investeerigu tulusust hinnata, on meil kõigepealt vaja välja selgitada mõned investeeringule iseloomulikud jooned. Me peaksime teadma:
- selle lõplikku väärtust,
- rahavoogude intervalle (kas investeerimine on perioodiline: näiteks igakuine),
- summasid, mida kavatsetakse kasutada
- ning investeeringu tootlust (%, mille jagu meie investeeringu väärtus tõuseks).
Ilma nende elementideta kompame me pimeduses ning ei suuda eeldada oma tulevikuväärtust isegi parima tahtmise juures.
Investeeringu lõppväärtuse ja rahavoogude intervalli puhul omab igaüks meist mingisugust aimdust nende suurusest. Teades oma sissetulekut, teame me, kui palju saame korraga investeerida. Samuti teame me, kas meile sobib investeerida ühe suure summa kaupa korraga või eelistame me investeerida väikestes osades järjepidevalt.
Küsimus võib aga tekkida tootlikkuse hindamisel. Kuidas teha seda objektiivselt? Kas võtta mõne indeksi perioodiline muutus aluseks? Majandusennustused? Võlakirjade ja intressi maksvate vahendite puhul on kõik lihtne – vaata nende fikseeritud määra ja sellega on kõik ammendatud. Kuidas aga hinnata seda tulemust aktsiate puhul?
Aktsiate puhul saaksime me rakendada dividenditootlust ning kasutada seda intressimäärana, kuid aktsiate hind on ajas muutuv ning dividendimäär võib sellisel juhul olla petlik. Kuigi dividendimäär on sarnane võlakirjade intressimäärale, erinevad aktsiad võlakirjadest selle poolest, et nende hind on mõjutatud ainult turutingimustest ning lõputult muutlik.
Võlakirjade hind võib muutuda ajas, kuid võlakirjad on ehitatud nii, et võlakirja väljamakse kuupäeval saab selle omanik kätte võlakirja nimiväärtuse summa, mitte turuhinna – ehk kui võlakirjade hind järelturul muutub, ei muuda see meie investeeringu väärtust (eeldusel, et me hoiame neid lõpetamiseni ning võlakirja hinna langus pole tingitud selle väljastaja pankrotist vms). Aktsiatel selline mehhanism puudub ehk kui aktsia hind langeb = otsene kahju meie portfellile, mille vastupidiseks pöördumisele puudub garantii.
Portfelli tootluse objektiivseks hindamiseks on mitmeid võimalusi ning ühte neist oleme varasemalt ka käsitlenud, kuigi tookord jäi ülevaade natukene üldiseks.
DCA (dollar cost averaging) on mudel, mille abil on võimalik luua ülevaade portfelli keskmisest tulususest võrreldes perioodi jooksul tehtud investeeringute kogukulu keskmisega. Tegemist on taaskord spekulatiivse näitajaga, mis loob eelduseid mineviku tulemustelt, kuid pikas perspektiivis on tegemist üpris hea funktsiooniga.
DCA on hea tööriist, kui me tegeleme varadega, millel puhul pole võimalik selget tootlust määrata. Samas on see hea tööriist, millega kontrollida oma eelarvet, eriti kui tegeleda perioodilise investeerimisega (näiteks 50€/kuus). Ühtlasi annab DCA eelise perioodilistele investeerijatele nende ees, kes investeerivad suurte osade kaupa.
Näiteks, kui indeks maksab täna 100€ ning me investeerime 1000€ sellesse korraga, tähendab, et me saame soetada täpselt 10 osakut indeksist.
Samas majandus on tsükliline ning indeksi hind võib aasta jooksul olla 90€, 110€ ja 100€. See tähendab, et perioodidel, kus indeksi osaku väärtus on üle 100€, oleme me kasumis, kuid hinna langedes oleme me miinuses.
Samas, kui me oleksime ostnud indeksi osakuid erinevatel ajaperioodidel, oleks meie tootlus stabiilsem, sest me ostaksime indeksi osakuid alguses 100€ eest, hinna langedes 90€ eest ning ostaksime osakuid, kui hind tõuseb üle 100€.
Kui ostud toimuvad erinevatel ajaperioodidel erineva hinna eest, kuid meie investeeritav summa on igal kuul sama, on tootlus palju stabiilsem.
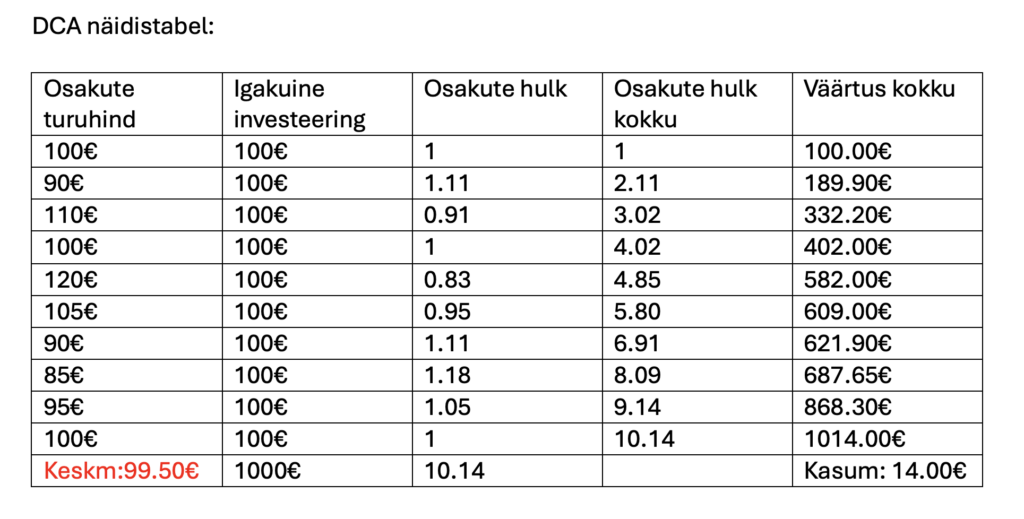
Näidise järgi on meie portfelli tootlikkuse protsent 1,4%/10 kuu jooksul.
Kui sama tehing oleks toimunud ühe ostuga 1000€, kui hind oli 100€/osak, oleksime saanud osakuid ainult 10tk ja oleksime investeeringuga nullis. Ostes osakuid erinevatel ajaperioodidel teenisime me kasumit perioodi muutuste pealt.
Lisaks sellele tõime me keskmise osaku hinna alla ligi 0.50€, mis on märkimisväärne, arvestades, et hind tõusis vahepeal 20%.
Selline lähenemine annaks eriti suure eelise dividende maksvate aktsiate puhul, sest sellised varad maksavad dividende iga omatud osaku eest ning pikas perspektiivis suudame me oma osakute hulka sedasi suurendada kiiremini, kui need investorid, kes investeerivad passiivselt.
Samas DCA võimekus on piiritletud. See töötab kasulikult ainult seni, kuni me oleme võimelised turu tegevust usaldusväärselt hindama. Kerge vaevaga võib arvestada teatud hinnakoridorid, kus aktsia on liikunud ning teha selle järgi kaalutletud otsuseid.
Majandustsükli käigus tuleb ette olukordi, kus hinnamuutused ei järgi trende ning tugevad müügilained või äkilised ostulained võivad saada saatuslikuks meie tootlusele, mistõttu pole DCA kõige usaldusväärsem tööriist. Samuti on miinuseks see, et DCA sõltub minevikus toimunust ning võib moonutada objektiivsust.
Neile, kes tahavad selgust saada oma portfelli realistlikust teenistusest, on see päris hea tööriist, mida rakendada. Tähelepanu tasuks pöörata eelkõige sellele, et minevikus toimunu ei ole tuleviku aluseks ning kasulik oleks DCA mudeleid korrigeerida täpsuse säilimiseks.
Kui me teame portfelli tootlust (hinnangulist), saame me planeerida edasist. Loo alguses sai mainitud liitintressi arvestust ja kuidas see ei tööta portfelli tulevikuväärtuse hindamisel, kui rakendada aktsia ajaloolist tulusust. Kuid DCA saab meid selles aidata, isegi kui tulemus on hüpoteetiline.
Järgnev on ülimalt spekulatiivne ning annab ainult kaudse tulemi võimaliku teenistuse kohta. Võrreldes aga erinevaid ajaperioode ning aktsia hinna muutuste protsent, saame me luua aritmeetilised keskmised erinevate kuude ja hinnamuutuste kohta.
See on suhteliselt ohtlik, sest me ei saa arvestada makromajanduslike muudatuste ja muu kvalitatiivse infoga, mis tähendab, et meie tulem on ohustatud majandusriskide poolt. Kuid me saame aluspõhja, millele ehitada tulevikuprognoosid – see on parem, kui täielik teadmatus. Tasub meeles pidada, et neid prognoose tuleks korrigeerida järjepidevalt ning oleks mõistlik võtta iga prognoosi konservatiivselt (eeldada, et tegelikkus on veel väiksem, kui numbrid näitavad).
Olles leidnud tootluse läbi DCA (hinnanguline tootlus) või kasutades reaalset tootlust, mis on garanteeritud fikseeritud sissetulekuobjektide poolt, saame nüüd rakendada liitintressi valemit ning leida portfelli tulevikuväärtuse.
Selleks on meil vaja teada ülalmainitud faktoreid: aeg, summa, investeeringu suurus ja tootluse %.
- Aeg = periood, mil tahame investeeringu lunastada,
- Summa = igal perioodil investeeritud summa (nt iga kuu kuni investeeringu lunastamiseni),
- Investeeringu suurus = kogusumma, mida soovime investeerida (oluline ainult siis, kui me investeerime ühes osas ning ootame lunastushetkeni),
- Tootluse % = kas hinnanguline %, mille me arvame teenivat või reaalne (garanteeritud instrumendi poolt).
Liitintressi saame portfelli hindamiseks rakendada peamiselt kahel viisil. Kui meie investeering on üheosaline, saame kasutada tavalist liitintressi valemit:

Selle näita puhul: investeerides 1 000€, 5. a perioodiga, tootlikkusega 5% = meie teenistus:
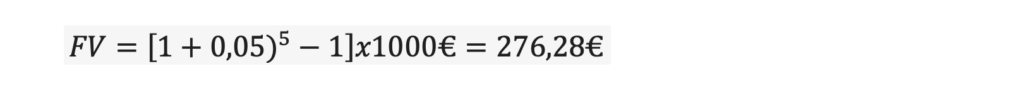
See tähendab, et 5 aasta pärast oleks meie portfelli väärtus 1 276,28€.
Kui me aga investeeriksime igakuiste osade kaupa, peaksime me rakendama annuiteedi valemit (annuiteet = osamakse, mis lisandub investeeringule ning mille intressid samuti liidetakse). Annuiteedi valem näeb välja selline:

Võttes aluseks eelneva näite saame me selle valemi järgi tulemuseks:
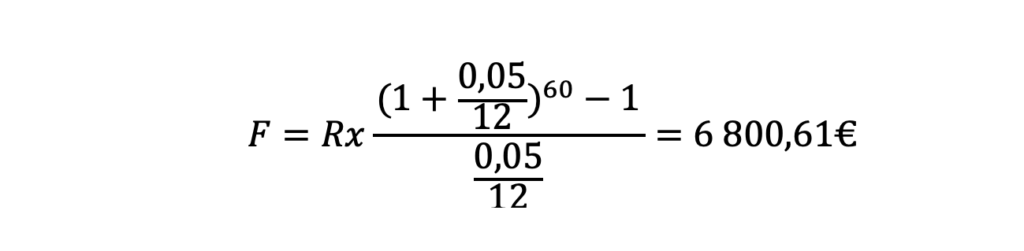
See tähendab, et selline oleks meie portfelli koguväärtus 5 aasta pärast.
Ainuüksi nende kahe tulemi võrdlusest on näha, et igakuine ja järjepidev investeerimine on kasulikum, kui investeerimine passiivselt ja suurte summadega. Seega, kes väidab, et investeerimisega alustamiseks on vaja palju raha, eksib.
Teades oma portfelli võimalikku tulevikuväärtust, võime siinkohal lõpetada ning olla endaga rahul. Sellise strateegia puhul oleme ju edukad? Kuid kuidas seda edu hinnata?
Ühe võimalusena tuleb meile siinkohal appi NPV, millega alustasime tänast lugu. Kuid kuidas seda rakendada? Sisuliselt võiksime võtta oma portfelli lõppväärtuse ning taandada selle NPV valemi abil nüüdisväärtusele.
Antud näide pole ideaalne, sest raha lisamine toimub perioodi jooksul, kuid jättes selle kõrvale, näeks meie investeeringu hindamise arvestus välja järgmine:
Kõigepealt arvestame sellega, et me peaksime kulutama 6 000€ 5 aasta jooksul ning saaksime perioodi lõpus tagasi 6 800,61€ (piltlikult öeldes: kujuta ette, et kulutad ära 6 000€. Seda ei ole enam, kuniks hiljem saad tagasi 6 800,61€).
Näite kohaselt peaksime me hindama oma algse investeeringu ja tuleviku lõppväärtuse ümber nüüdisväärtusesse.
See tähendab, et: 6000 / 1,055 = 4 701,16.
Järgmiseks peame leidma oma tuleviku investeeringu nüüdisväärtuse: 6 800,61 / 1,055 = 5 328,46.
Kui me tulemused lahutame (lõppväärtus – algne investeering), näeme, kas meie investeering on tulus või mitte: 5328,46 – 4701,16 = 627,30. Kuna antud investeeringu puhul on tulemus positiivne, saame öelda, et tegemist on tulutoova investeeringuga.
Miks me võtame algsumma samuti nüüdisväärtusele? Miks me ei jäta seda algsesse vormi? Sisuliselt võiksime me seda teha ning see oleks mõistlik, kui me räägiksime olukorrast, kus me ostame selle raha eest mingi tulutoova objekti (näiteks tootmisseadme) kohe ja praegu ning see hakkab meile tulevikus tootma rahavoogusid.
Antud juhul tahame võrrelda kahe erineva objekti kasulikkust – kumb on kasulikum:
a) raha kogumine panka või
b) raha perioodiline investeerimine.
Kuigi aeg raha väärtust ei mõjuta, mõjutavad selle ostuvõimet turutingimused (eelnev iPhone’i näide) ja möödalastud võimalused. Seega realistliku ülevaate saamiseks oleks mõistlik võrrelda mõlemat rahahulka nüüdisväärtusel.
Näitega edasi minnes, kas see ongi kõik? Sisuliselt oleme me leidnud netonüüdisväärtuse tingimusel, et saame kogu investeeritud summa kätte perioodi lõpus, kuid meie investeering eeldab igakuist investeeringut. See tähendab, et peame rakendama mingisugust meetodit, mis võtaks arvesse perioodilisust, et meie arvestus oleks objektiivne.
Perioodilise arvestuse jaoks on mitu võimalust. Kõige pikem ja keerulisem neist on neto nüüdisväärtuse kasutamine rakendades seda kõigile investeerimisperioodidele.
See tähendab, et me peame leidma:
1) perioodilise rahavoo,
2) perioodilise intressimäära.
Perioodilise intressimäära saame me arvestada välja lihtsalt valemiga:
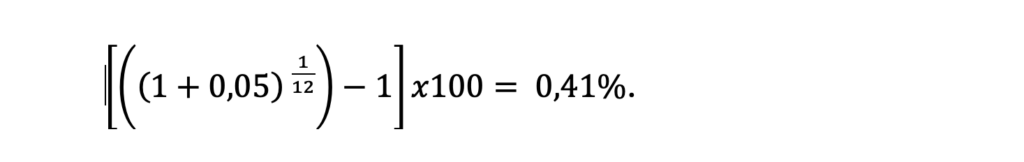
See valem jagab aastase intressimäära ära perioodide vahel, milleks meie näites on 1 kuu. Kuna meie sissemaksed investeeringusse on igakuised, on õiglane jagada intressimäär samuti kuude lõikes ära.
Perioodilise rahavoo leidmine on aga natukene keerukam. Perioodiline rahavoog eeldab, et me teame oma igakuiseid sissemakseid ning laekuvat intressitulu. Intressitulu on aga meie näite puhul eksponentaalselt kasvav – mida suurem on meie investeerimisportfell, seda suurem on tulu sellel ajahetkel. Matemaatiliselt on võimalik arvutada rahavoogusid ajas, teine võimalus on võtta eeldatav intressitulu ja jagada see perioodide peale ära (800,61€ / 60).
Mõlemad variandid tehniliselt töötavad, kuid kindlasti saame täpsema vastuse, kui leiame konkreetse perioodilise tootluse. Üheks võimaluseks on rakendada annuiteedi valemit perioodiliselt. See tähendab, et me hakkame annuiteedi kordajat vähendama vastavalt sellele, kui mitu perioodi meil veel investeeringust järel on.
See oli antud näites tavaline annuiteedi valem:
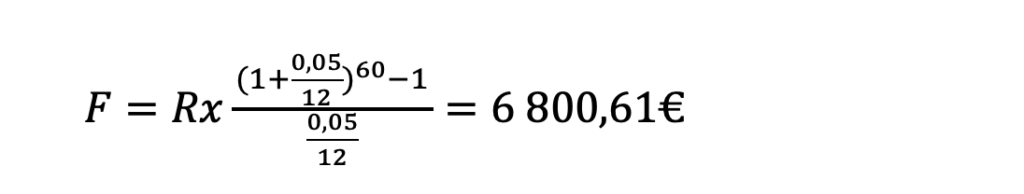
Nüüd muudame seda, asendades astmel 60 järelejäänud kuude arvuga. Teisisõnu, kui me oleme esimese aasta investeerinud ära ning soovime leida ülejäänud perioodide tootluse, siis me võtame algse astendaja 60 ning lahutame sellest 12 (1. aasta kuud) ning saame uue valemi:
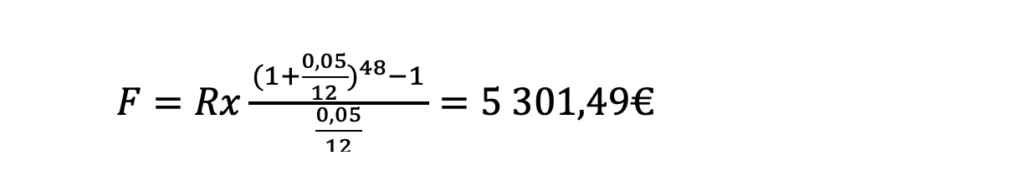
Sedasi jätkame, kuni oleme taandanud astendajad 12-ni. Saadud tulemustest lahutame selleks perioodiks investeeritud summad ning lõpuks lahutame viimasest tulemusest eelmise, et saada perioodi rahavoog.
Selguseks võib vaadata järgmist tabelit:
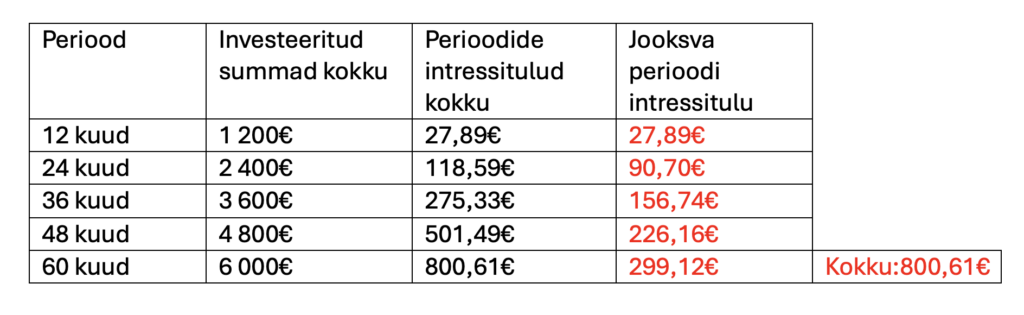
Olles leidnud otsitavad rahavood, saame need jagada aastate kaupa 60 kuu peale, et need järjest neto nüüdisväärtusele tuua. Selline hulk kalkulatsioone käsitsi teha on aeganõudev ning ebapraktiline, aga õnneks on Excelisse sisse ehitatud funktsioon, mis suudab selle arvutuse meile ära teha. Kui tahta, võib käsitsi arvutada ning selle jaoks kasutada eelnevalt mainitud valemeid. Kui me arvestame neto nüüdisväärtust 60 kuu kohta, siis selle jaoks tuleks intressimäärana rakendada eelnevalt arvestatud perioodilist intressimäära (0,41%).
Arvestada tasub sellega, et perioodilise jaotuse puhul tekivad ümardusvead, mis võivad lõpptulemust mõjutada mõne euro võrra. See ei ole oluline viga, kuid täpsema vastuse saamiseks tasub jätta vastusele rohkem komakohti.
Perioodilise jaotusega tuli sellise investeeringu neto nüüdisväärtuseks 5 988,14€. Mida sellest järeldada? Järelduste loomiseks peaksime me taaskord viima oma algse investeeringu neto nüüdisväärtusele ning võrdlema tulemusi. Kasutades sama Exceli funktsiooni ja intressimäära leiame oma põhiosade nüüdisväärtuse, milleks on 5 309,38€. See tähendab, et 5 988,14 – 5 309,38 = 678,76€. Arvestades, et tulemus on positiivne, saame me öelda, et selline investeering oleks tulus.
Siinkohal tuleb erilist tähelepanu pöörata järgnevale:
a) meil pole täna 6 000€,
b) kogudes 100€ maksetega selle kokku, on see tulevikus vähem väärt, kui perioodiliselt investeerides.
Sama võib sisuliselt öelda näiteks filosoofia kohta: „parem on koguda ja investeerida suuremates summades, kui teha seda väikeste summade kaupa“ – neto nüüdisväärtusega saab tõestada ära, et see ei ole tõsi.
Kuigi näiteks lühikeste perioodide puhul (aasta ja vähem) ei ole erinevus märgatav, jääb mõte samaks – järjepidev tegevus on parem ootamisest.
Ootamine on üldse paradoksaalne, kas pole nii? Millal on mõistlik oodata? Millal peaksime tegutsema? Lõppude lõpuks taandub kõik planeerimisele. Olles planeerinud oma tegevuse ja kaalunud erinevaid variante ning võimalikke tulemeid omavahel, ei pea me tuginema ainult vanasõnadele nagu: „ootamine ja kannatlikkus on voorused“, vaid me teame, et võime liikuda edasi enesekindlusega, mille aluseks on selge plaan.
#ElaEksponentaalselt

